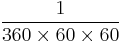Small number
Within a set of positive numbers, a number is small if it is close to zero. A number is smaller if it is less than another number.
Within a set of positive and negative numbers there is ambiguity, because being closer to zero does not correspond to being less, but to being less in absolute value. Depending on context a negative number may be called "smaller" if it is closer to zero, or if it is more negative.
This article deals with positive numbers, and is also applicable to negative numbers by taking the absolute value.
Small numbers are numbers that are small compared with the numbers used in everyday life. Very small numbers often occur in fields such as chemistry, electronics and quantum physics.
Contents |
Fractions
As soon as systems of weights and measures were devised, units were subdivided into smaller units: pounds were divided into ounces, pounds into shillings and pence. Beyond the smallest units, there was a need to use vulgar fractions to represent even smaller quantities. In systems such as the degrees-minutes-seconds system, it is possible to represent one second of arc, equal to
of a circle.
Tiny numbers in science
Even smaller numbers are often found in science, which are so small that they are not easily dealt with using fractions. Scientific notation was created to handle very small and very large numbers.
Examples of small numbers describing everyday real-world objects are:
- size of a bit on a computer hard disk
- feature size of a structure on a microprocessor chip
- wavelength of green light: 5.5 × 10-7 m
- period of a 100 MHz FM radio wave: 1 × 10-8 s
- time taken by light to travel one meter: roughly 3 × 10-9 s
- radius of a hydrogen atom: 2.5 × 10-11 m
- the charge on an electron: roughly 1.6 × 10-19 C (negative)
Other small numbers are found in particle physics and quantum physics:
- size of the atomic nucleus of a lead atom: 7.1 × 10-15 m
- the Planck length: 1.6 × 10-35 m
Extremely small numbers
Extremely small numbers can be described through their reciprocal, an extremely large number. The notation is similar, with a minus sign at the first level of exponents, e.g.
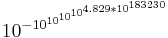
Infinitesimals
Although all these numbers above are very small, they are all still real numbers greater than zero. Some fields of mathematics define infinitesimal numbers. An infinitesimal is a number greater than zero yet smaller than any positive real number.
Infinitesimal numbers were originally developed to create the differential and integral calculus, but were replaced by systems using limits when they were shown to lack theoretical rigor. More recent work has restored rigor to infinitesimals, making them once more a legitimate mathematical topic (see non-standard analysis).
Systems of infinitesimals can be generated in the same way as systems of transfinite numbers can be generated. Some mathematical systems such as surreal numbers and hyperreal numbers generate elaborate systems of infinitesimals with amazing properties.